[COVID-19] DỰ ĐOÁN DỊCH COVID-19 Ở HÀ NỘI

Chúng ta đang sống trong một thế giới mà tất cả mọi người phải ngồi im một chỗ, các nhân viên y tế trong bộ quần áo và mũ bảo hộ chẳng khác gì trên trạm không gian vũ trụ, mỗi buổi sáng ngủ dậy ai cũng nhìn vào màn hình điện thoại để tìm kiếm con số thống kê người nhiễm và người tử vong của ngày hôm trước.

Ngay cả hơi thở của chúng ta cũng bị vi-rút tấn công.

Thủ đô Hà Nội, nơi cách Đà Nẵng gần 800km, mặc dù chưa thấy cảnh tương tự ở thành phố biển miền Trung, nhưng đã xuất hiện 11 bệnh nhân COVID (trong đó có 9 ca liên quan đến Đà Nẵng). Sau ca bệnh được công bố đêm qua, chính quyền đã đưa ra khuyến cáo giãn cách nhà hàng bia và quán cà phê bắt đầu từ 0 giờ đêm nay, khuyến cáo toàn dân nếu không có việc cần thiết không ra khỏi nhà.

Vậy tình hình dịch bệnh thời gian tới sẽ như thế nào?

Có 2 cách để dự báo mức độ lây lan của dịch bệnh: một là dựa vào những kinh nghiệm trong quá khứ, hai là xây dựng mô hình toán học; hầu hết các quốc gia trên thế giới dựa vào cách thứ 2.

Nguyên lí của mô hình toán học không quá phức tạp.

Là một bác sĩ Xquang hạng 3, không phải chuyên ngành về dịch tễ học, cũng không phải là người chuyên về toán, nhưng tôi muốn biết diễn biến từng ổ dịch có thể xảy ra với quy mô như thế nào, vì thế mà ngay từ đầu vụ dịch tôi đã tự tìm hiểu mô hình SEIR, đây là mô hình dịch tễ cơ bản nhất được Kermack và McKendrick xây dựng từ năm 1927, bất cứ ai làm về phòng chống dịch cũng biết mô hình này.

🍁🍁🍁🍁🍁🍁

SEIR là viết tắt của các chữ cái đầu tiên.

👉 S = susceptible (nhạy cảm): Được hiểu là những người chưa có kháng thể chống lại vi-rút, họ tiếp xúc với bệnh nhân COVID, nên có khả năng bị lây bệnh.

👉 E = exposed (ủ bệnh): Là những người đã nhiễm vi-rút nhưng chưa phát bệnh. Thời gian ủ bệnh trung bình kí hiệu là TE.

👉 I = infectious (lây nhiễm): Là những bệnh nhân đã phát bệnh và có nguy cơ lây bệnh cho người khác. Thời gian lây nhiễm trung bình kí hiệu là TI.

👉 R = recovered (đã miễn nhiễm): Là những bệnh nhân đã khỏi bệnh hoặc chết.

Hiểu đơn giản là bất kì ai trong chúng ta đều có thể trải qua các giai đoạn COVID gồm: GĐ nhạy cảm 👉 GĐ ủ bệnh 👉 GĐ lây nhiễm 👉 GĐ hết bệnh.

Mở rộng ra với cộng đồng N cá thể có nguy cơ:

N = S + E + I + R

Hoặc:

N = = S(t) + E(t) + I(t) + R(t)

🍁🍁🍁🍁🍁🍁

Xác định hệ só lây nhiễm cơ bản R0.

λ = lnY(t) / t

Trong đó t là thời gian tích lũy số ca bệnh Y(t) từ điểm xuất phát đến thời điểm tính toán.

Tg = 1 / γ1
TI = 1 / γ2
Tg = TE + TI
ρ = TE / Tg

Công thức tính hệ số lây nhiễm cơ bản R0:

R0 = (1 + λ / γ1) (1 + λ / γ2)

Hoặc:

R0 = 1 + λTg + p(1 – p)( λTg)ᴧ2

 

☂️ DỮ LIỆU BỆNH NHÂN CỦA HÀ NỘI

– Bệnh nhân: Là những ca bệnh sinh sống ở Hà Nội có, số bệnh nhân được mã hóa theo Bộ Y tế.

– Thời điểm nhiễm: Ngày tiếp xúc nguồn lây.

– Thời điểm khởi phát: Ngày xuất hiện triệu chứng đầu tiên.

– Thời gian ủ bệnh: TE được tính theo từng bệnh nhân. Với 3 bệnh nhân không có triệu chứng (BN 459, BN 969 và BN 979) nhưng có yếu tố dịch tễ nên xét nghiệm rt-PCR dương tính, vậy tôi chọn thời gian ủ bệnh TE = 5 ngày, theo như một số nghiên cứu trên thế giới về COVID.

– Thời gian lây nhiễm: Do từng bệnh nhân điều trị chưa công bố kết quả khi nào vi-rút không thể lây nhiễm, nên tôi tạm chọn thời gian trung bình TI = 14 ngày, dựa trên một số nghiên cứu của thế giới.

👉 BN 447
– Thời điểm nhiễm: 12/7
– Thời điểm khởi phát: 23/7.
– Thời gian ủ bệnh: TE = 11 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 45/4.

👉 BN 459
– Thời điểm nhiễm: 21/7
– Thời điểm khởi phát: 26/7 (tạm dự đoán)
– Thời gian ủ bệnh: TE = 5 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 18/5.

👉 BN 714
– Thời điểm nhiễm: 14/7
– Thời điểm khởi phát: 19/7
– Thời gian ủ bệnh: TE = 5 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 68/10.

👉 BN 752
– Thời điểm nhiễm: 24/7
– Thời điểm khởi phát: 2/8
– Thời gian ủ bệnh: TE = 9 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 8/2.

👉 BN 785
– Thời điểm nhiễm: 16/7
– Thời điểm khởi phát: 3/8
– Thời gian ủ bệnh: TE = 18 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 20/4.

👉 BN 812
– Thời điểm nhiễm: 27/7
– Thời điểm khởi phát: 3/8
– Thời gian ủ bệnh: TE = 7 ngày.
– Số người tiếp xúc trực tiếp/số ngày = chưa rõ.

👉 BN 962
– Thời điểm nhiễm: 20/7
– Thời điểm khởi phát: 10/8
– Thời gian ủ bệnh: TE = 21 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 5/2.

👉 BN 969
– Thời điểm nhiễm: 8/8
– Thời điểm khởi phát: 13/8 (tạm dự đoán)
– Thời gian ủ bệnh: TE = 5 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 0/0.

👉 BN 979
– Thời điểm nhiễm: 22/7
– Thời điểm khởi phát: 27/7 (tạm dự đoán).
– Thời gian ủ bệnh: TE = 5 ngày.
– Số người tiếp xúc trực tiếp/số ngày = 52/8

Thời gian ủ bệnh TE nếu cỡ mẫu đủ lớn sẽ tuân theo hàm phân phối chuẩn, bởi vệ tôi tính theo trung bình mẫu.

TE = ΣnTEi / 9
TE = (4×5+7+9+11+18+21):9 = 10 (ngày).

Mốc thời gian bắt đầu xuất hiện dịch, tôi căn cứ BN 447, có ngày đi du lịch Đà Nẵng sớm nhất trong số 9 bệnh nhân, bắt đầu từ trưa 12/7 với lịch trình 3 ngày 2 đêm.

☂️ TÌNH HỆ SỐ LÂY NHIỄM CƠ BẢN R0

– Thời gian: t = 37 ngày (từ 12/7 – 17/8).
– Số lượng bệnh nhân tích lũy: Y(t) = 9

Vậy ta có: λ = lnY(t) / t = ln9 / 37 = 0,0595
Mặt khác: Tg = TE + TI = 10 + 14 = 24 ngày.
Nên ta có: p = TE / Tg = 10:24 = 0,4167

Thay λ = 0,0595; Tg = 24; p = 0,4167 vào công thức R0 ta được.

R0 = 1 + 0,0595×24 + 0,4167x(1 – 0,4167)(0,0595×24)ᴧ2 = 3

👉 Như vậy, ở thời điểm hiện tại, hệ số lây nhiễm cơ bản của Hà Nội tôi ước tính R0 = 3, nghĩa là mỗi người có nguy cơ lây nhiễm cho 3 người.

🍁🍁🍁🍁🍁🍁

👉 Nếu giữ con số R0 = 3, để dịch bệnh tiếp tục lây nhiễm không tăng cường các biện pháp kiểm soát, thì tỉ lệ người nhiễm đạt đến miễn dịch cộng đồng sẽ là = (1 – 1 / R0) = 67% dân số Hà Nội.

👉 Xác suất lây nhiễm của mỗi người tiếp xúc trực tiếp với bệnh nhân (F1) được tính theo công thức:

b = R0 / kTI

Trong đó k là số lần người tiếp xúc trung bình mỗi ngày của bệnh nhân lây nhiễm. Cụ thể với 8 bệnh nhân có số liệu tiếp xúc, thì k = 6. Như vậy xác suất mỗi F1 có khả năng lây nhiễm là b = 3,6%.

👉 Áp dụng các biện pháp giãn cách xã hội.

Thực hiện duy trì khoảng cách an toàn trên 2m, thực hiện đeo khẩu trang, rửa tay xà phòng, đó là những biện pháp phòng bệnh hiệu quả. Ngoài ra, các biện pháp giãn cách xã hội như hủy bỏ các cuộc tụ tập đông người, giảm tiếp xúc xã hội, đều nhanh chóng hạ thấp hệ số lây nhiễm.

Gọi f là tỉ lệ dân số tham gia thực hiện giãn cách xã hội, a là tỉ lệ phần trăm tiếp xúc đã giảm xuống, R là hệ số lây nhiễm đã được giảm xuống; thì công thức cơ bản là.

R = [1 – (1-aᴧ2)f]R0

Ví dụ, khoảng f = 30% dân số thực hiện giãn cách, giảm tiếp xúc a = 40%, thì hệ số lây nhiễm R0 = 3 sẽ giảm xuống R = [1 – (1-0,4×0,4)x0,3]x3 = 2,2 và như vậy sau một chu kì 14 ngày vẫn còn phải tiếp tục chờ đợi. Chu kì 14 ngày tiếp R = [1 – (1-0,4×0,4)x0,3]x2,2 = 1,6 dịch vẫn chưa giảm. Tiếp tục thêm 14 ngày nữa R = [1 – (1-0,4×0,4)x0,3]x1,6 = 1,2 vẫn còn tăng nhẹ. Tiếp thêm 14 ngày nữa R = [1 – (1-0,4×0,4)x0,3]x1,2 = 0,9 < dịch đã được khống chế và hết dần.

Như vậy nếu 30% dân số thực hiện giảm tiếp xúc 40% thì Hà Nội sẽ cần 64 ngày để khống chế thành công dịch.

Ví dụ, khoảng f = 70% dân số thực hiện giãn các, giảm tiếp xúc a = 50%, thì sau một chu kì 14 ngày sẽ giảm hệ số lây nhiễm R = [1 – (1-0,5×0,5)x0,7]x3 = 1,4 vẫn chưa khống chế được dịch. Tiếp tục 14 ngày hệ số lây nhiễm R = [1 – (1-0,5×0,5)x0,7]x1,4 = 0,7 < 1 nên chỉ gần 1 tháng đã khống chế thành công đợt dịch.

🍁🍁🍁🍁🍁🍁

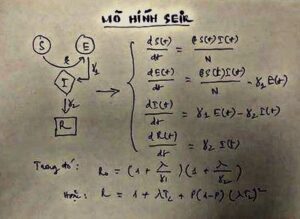
Xem xét phương trình vi phân của mô hình SEIR.

🍀 PHƯƠNG TRÌNH VI PHÂN THỨ NHẤT

dS(t) / dt = βS(t)I(t) / N

Phương trình này dùng để mô tả sự thay đổi của số người nhạy cảm S.

Về mặt lí thuyết, nếu hệ số lây nhiễm cơ bản R0 > 1, nó sẽ lây nhiễm cho hầu hết mọi người nếu không có biện pháp phòng chống và kiểm soát. Số lượng quần thể mẫn cảm S ngày càng nhỏ, thì tốc độ lây truyền sẽ càng giảm, do khả năng những người trong thời kì lây nhiễm I tiếp xúc với quần thể mẫn cảm S sẽ giảm đi, vì vậy mô hình lí thuyết cần mô tả số lượng quần thể mẫn cảm S.

Tuy nhiên, trong thực tế dịch ở Hà Nội cả 10 ca đều có yếu tố dịch tễ liên quan đến Đà Nẵng, tỉ lệ người mắc bệnh trong tổng dân số là rất nhỏ, số người mẫn cảm S có thể được coi là không đổi, bằng tổng dân số, nghĩa là S (t) = N.

Do đó, phương trình vi phân này có thể được bỏ qua, không cần thiết phải áp dụng tính toán với Hà Nội.

🍀 PHƯƠNG TRÌNH VI PHÂN THỨ HAI

dE(t) / dt = βS(t)I(t) / N – γ1E(t)

Phương trình vi phân này có ý nghĩa mô tả sự thay đổi của quần thể đã nhiễm vi-rút nhưng đang trong thời kì ủ bệnh E trên một đơn vị thời gian bằng với lần nhiễm mới được thêm vào trừ đi số lần chuyển từ giai đoạn ủ bệnh sang giai đoạn lây nhiễm.

Điều đó được thể hiện dễ hiểu như sau:

E(t) – E(t – 1) = βI(t – 1) – γ1E(t – 1)

Trong đó β là số ca nhiễm trung bình trên một bệnh nhân trong một đơn vị thời gian, sau đó, có bao nhiêu trường hợp có thể bị nhiễm trong toàn bộ thời kì lây nhiễm đó chính là một dạng định nghĩa của hệ số lây nhiễm cơ bản R0.

🍀 PHƯƠNG TRÌNH VI PHÂN THỨ BA

dI(t) / dt = γ1E(t) – γ2I(t)

Phương trình này là sự thay đổi số ca bệnh trong thời kỳ lây nhiễm I trên một đơn vị thời gian. Nó được tính bằng số người mới chuyển từ thời kỳ ủ bệnh sang thời kỳ lây nhiễm, trừ đi số người chuyển sang trạng thái cách li từ thời kì lây nhiễm.

Phương trình này cũng được thể hiện dưới dạng rời rạc:

I(t) – I(t – 1) = γ1E(t – 1) – γ2I(t – 1)

🍀 PHƯƠNG TRÌNH VI PHÂN THỨ TƯ

dR(t) / dt = γ2I(t)

Phương trình này thể hiện số người bị cách ly trong một đơn vị thời gian bằng với số người mới được thêm vào trạng thái cách ly từ giai đoạn lây nhiễm.

Dạng rời rạc của nó là:

R(t) – R(t – 1) = γ2I(t – 1)

Từ 3 phương trình vi phân rời rạc, phản ánh mối quan hệ lặp của 3 đại lượng ở 3 trạng thái, tức là nếu biết tất cả các giá trị của tham số, ta có thể suy ra giá trị tại thời điểm t từ thời điểm t-1, và xác định điểm bắt đầu cho đến toàn bộ quá trình dịch bệnh.

Lưu ý rằng:

β = R0 / TI

γ1 = 1 / TE
γ2 = 1 / TI

Mô hình toán học SEIR xin xem trong ảnh minh họa, gồm 4 phương trình vi phân, khi giải chỉ cần lấy tích phân cả 2 vế mỗi phương trình, học sinh lớp 12 giải phương trình này dễ dàng, sinh viên đại học hoàn toàn có thể lập được phương trình vì nó thực sự không khó; vì thế tôi dành cho bạn đọc tự giải, để góp vui với bài viết này.

🍁🍁🍁🍁🍁🍁

KẾT LUẬN
————

👉 Dịch bệnh ở Hà Nội tôi ước tính hệ số lây nhiễm cơ bản R0 = 3.

👉 Nếu mong muốn có miễn dịch cộng đồng, thì phải 67% dân số Hà Nội mắc bệnh, điều đó dẫn tới hệ thống y tế không đủ sức chịu đựng, nên vẫn phải tích cực chống dịch.

👉 Mỗi người dân Hà Nội tiếp xúc F1 có xác suất lây nhiễm theo ước tính của tôi khoảng 3,6%.

👉 Áp dụng các biện pháp giãn cách xã hội như hủy bỏ tụ tập đông người, không có việc không nên ra khỏi nhà, phòng bệnh cá nhân (đeo khẩu trang, rửa tay dưới vòi nước chảy, giữ khoảng cách 2m khi tiếp xúc) là những biện pháp rất hiệu quả để phòng bệnh.

– Nếu 30% dân số Hà Nội tham gia giảm tiếp xúc 40% thì sau hơn 2 tháng Hà Nội sẽ an toàn.

– Nếu 70% dân số Hà Nội tham gia giảm tiếp xúc 50% thì sau gân 1 tháng Hà Nội sẽ an toàn.

👉 Hà Nội cần thực hiện phòng chống dịch.

– Xét nghiệm sớm những người có yếu tố nguy cơ (đi về từ vùng dịch, F1 và F2) để phát hiện sớm những ca bệnh.

– Kiểm soát chặt chẽ những nơi có nguy cơ bùng dịch (không gian kín, nhiệt độ thấp, mật độ người đông) như quán bar, vũ trường, hộp đêm, tụ điểm karaoke, nhà hàng, các nhà máy đông lạnh.

– Kiểm soát chặt chẽ bệnh viện bằng cách giảm tải bệnh nhân, bắt buộc phải tuân thủ quy trình chống nhiễm khuẩn bệnh viện, đảm bảo an toàn phòng bệnh (mở cửa, bật quạt thông gió, hạn chế điều hòa nhiệt độ, không để bệnh nhân nằm ghép, hạn chế người nhà bệnh nhân trong bệnh phòng). Thực hiện khám sàng lọc COVID với tất cả bệnh nhân ho, sốt, có các triệu chứng giống như cảm cúm, ban và xuất huyết dưới da. Bảo vệ nhóm bệnh nhân cao tuổi, bệnh nhân mắc các bệnh mãn tính (tăng huyết áp, tiểu đường, tim mạch, bệnh hô hấp mãn tính, suy thận, bệnh gan, các bệnh về máu).

– Bảo vệ những người có nguy cơ ngoài cộng đồng: Nhóm bệnh nhân có nguy cơ, những người làm việc phải thường xuyên tiếp xúc với công chúng.

– Bảo vệ nhân viên y tế.

🍀🍀🍀 TÔI TIN HÀ NỘI TIẾP TỤC AN TOÀN với số bệnh nhân không quá đầu ngón tay của vài bàn tay!

Nguồn: Bs. Trần Văn Phúc